WORKS
円形・円筒断面の耐力計算方法について
円形断面と薄肉円筒断面の軸力および曲げモーメントの公式の導入を示します。
厚肉の円筒断面の断面計算は、径の異なる円形断面の差を用いて計算します。
薄肉の円筒断面は鉄筋コンクリートの鉄筋の等価断面や鋼管などで使用します。
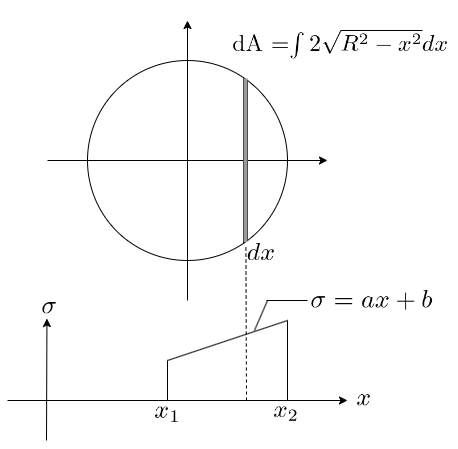
円形断面
$$ N = \int_{x1}^{x2} \sigma (x) \cdot A(x) dx $$
$$ =\int (ax+b) \cdot \sqrt{R^2 - x^2} dx $$
$$ = \left[ -\dfrac{a}{3} ( R^2 - x^2 )^ \dfrac{3}{2} + \dfrac{b}{2} \biggl( R^2
\cdot \sin^{-1} \dfrac{x}{R} + R \cdot x \cdot \sqrt{ 1 - \dfrac{x^2}{R^2}}
\biggr) \right]_{x1}^{x2} $$
$$ M = \int_{x1}^{x2} x\cdot \sigma (x) \cdot A(x) dx $$
$$ =\int_{x1}^{x2} (ax+b) \cdot x \cdot \sqrt{R^2 - x^2} dx $$
$$ = \left[ \dfrac{a}{8} \{ R^4 \sin^{-1}\dfrac{x}{R} - x \cdot \sqrt{R^2-x^2}
\cdot (R^2-2 \cdot x^2)\} - \dfrac{b}{3} ( R^2 - x^2 )^\dfrac{3}{2} \right
]_{x1}^{x2} $$
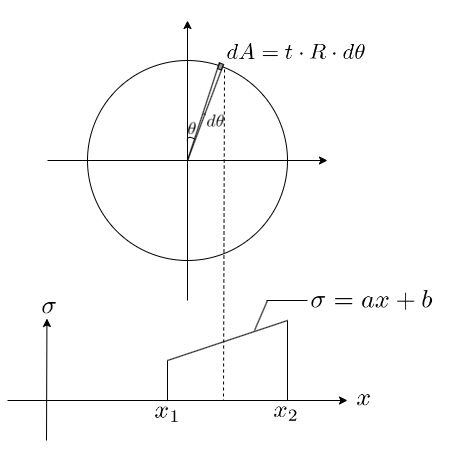
薄肉円筒断面
$$ N = \int_{\theta 1}^{\theta 2} \sigma (x) \; dA $$
$$ = \int_{\theta 1}^{\theta 2} \sigma (x) \cdot t \cdot R \; d\theta $$
$$ =\int ( ax+ b )\cdot t \cdot R \; d\theta $$
$$ =\int ( a\cdot t \cdot R^2 \sin \theta + b \cdot t \cdot R ) \; d\theta $$
$$ =\left[ -a\cdot t \cdot R^2 \cos \theta + b \cdot t \cdot R \cdot \theta \;
\right]_{\theta 1}^{\theta 2} $$
$$ M = \int_{\theta 1}^{\theta 2} x\cdot \sigma (x) \; dA $$
$$ =\int (ax+b) \cdot x \cdot t \cdot R \; d\theta $$
$$ =\int (atRx^2+btRx) \; d\theta $$
$$ =\int (atR^3 \sin^2 \theta + btR^2 \sin \theta) \; d\theta $$
$$ =atR^3 \int \sin^2 \theta + btR^2 \int \sin \theta \; d\theta $$
$$ =atR^3 \int \dfrac {1-\cos2\theta}{2} + btR^2 \int \sin \theta \; d\theta $$
$$ =atR^3 \left [ \dfrac{\theta}{2} - \dfrac{\sin2\theta}{4} \right]_{\theta
1}^{\theta 2} - btR^2 \left[\; \cos \theta \; \right]_{\theta 1}^{\theta 2} $$
